体彩排列五开出“55555”这一特定号码的概率为1/100000，这一结果基于简单的概率计算：每位数字从0到9随机选择，每位有10种可能，因此五位数组合共有10^5=100000种，每个组合出现的概率均等，“55555”只是其中之一，尽管该号码看似特殊，但数学上其中奖概率与“12345”或任何其他组合完全相同，彩票中奖是小概率事件，所有号码的数学概率均等，理性购彩至关重要。

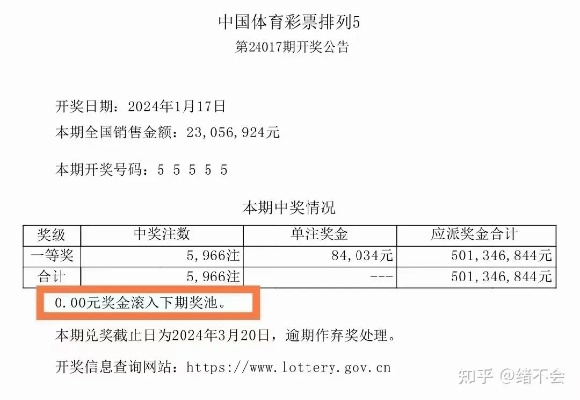
中国体育彩票“排列5”玩法开出了令人震惊的号码“55555”，一等奖中奖注数高达5万注，总奖金达到5亿元，这一事件迅速引爆网络，许多人惊叹于这种极端号码的出现，也有人质疑其背后的概率与公正性，体彩开出“55555”的概率究竟有多大？本文将从数学、统计学和彩票机制的角度，为你详细解析。

排列5的规则与概率计算

体育彩票“排列5”是一种数字型彩票玩法，玩家从00000到99999中选择一个5位数号码，开奖时随机摇出一个5位数作为中奖号码，如果所选号码与开奖号码完全一致（顺序相同），即中得一等奖，单注奖金10万元。

每个位置上的数字可以是0到9中的任意一个,且每个数字出现的概率在理论上相互独立，任何一个特定号码（例如12345或55555）被摇出的概率是相同的，计算如下：

• 每个数字有10种可能（0-9），5个数字组合的总数为 (10^5 = 100,000)。
• 开出“55555”的概率是 (1/100,000)，即十万分之一。

这个概率看似极低,但需要注意的是，在随机事件中，任何号码出现的概率都是均等的。“55555”与其他号码（如12345或00000）并无本质区别，只是人类心理倾向于关注“特殊模式”（如重复数字、对称数字等），从而觉得其异常罕见。

概率的直观理解：到底有多难？

十万分之一的概率是什么概念？我们可以通过一些类比来理解：

• 你连续抛掷一枚公平硬币17次,全部正面朝上的概率约为 (1/131,072)，与十万分之一接近。
• 买一注“排列5”中得一等奖的概率，比北京小客车摇号中签的概率（2023年约为0.3%）还要低200倍。
• 如果每天买一注,平均需要约274年才能中一次一等奖（假设每天开奖）。

但概率学中有一个常见的误解：小概率事件并非不会发生，在大量试验中，极端事件出现的可能性甚至会增加，排列5每年开奖365次，每期有100,000种可能号码，因此理论上“55555”这类号码平均每274年会出现一次（但实际是随机分布，可能更早或更晚）。

为什么这次开出让人们感到震惊？

尽管概率均等,但“55555”的出现仍引发了广泛讨论，原因主要有三：

1. 心理偏差：人类大脑对重复、对称模式特别敏感，会潜意识地认为“55555”比普通号码更罕见，所有号码的概率相同，但人们更容易记住“特殊事件”。
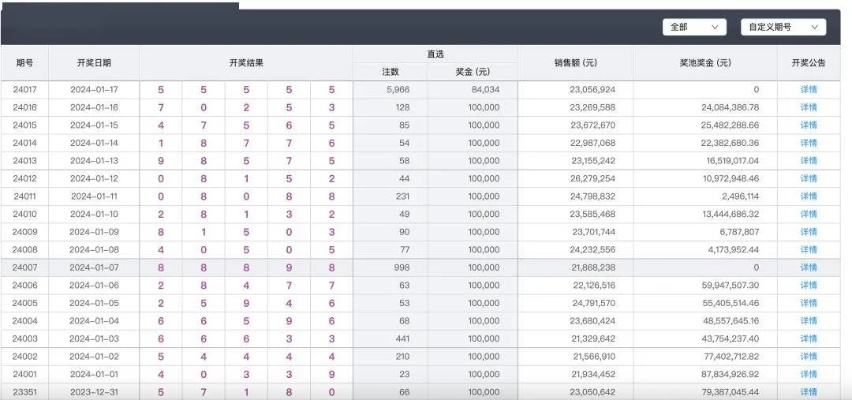
2. 中奖注数异常：本次开奖共有5万注一等奖，远高于往常（通常仅几注到几十注），这是因为许多彩民偏爱“豹子号”（重复数字），导致投注高度集中，但中奖人数多并不影响号码本身的随机性——开奖机制是独立的。
3. 对公平性的质疑：有人怀疑开奖是否被人为操纵，但根据中国体彩的规则，开奖使用物理摇奖机（如吹气式摇奖球）或电子随机数发生器，并经过公证机构监督，从数学上看，极端号码的出现恰恰证明了随机性（反之，如果永远避开“特殊号”，反而可能可疑）。

统计学视角：小概率事件必会发生

在概率论中,“无限猴子定理”形象地说明：只要时间足够长，小概率事件几乎必然发生，排列5自2004年发行以来，已开奖超7000期，计算显示：

• 截至2024年,排列5历史开奖号码总数约7000个。
• “55555”未出现的概率为 ((99,999/100,000)^{7000} \approx 93.2\%)，即仍有约6.8%的概率在此前出现过一次，本次开出并不算“违背概率”。
• 类似号码曾多次出现：例如2019年开过“00000”，2021年开过“99999”，其他重复数字（如“11111”“22222”等）也均有历史记录。

理性看待彩票：数学与娱乐的平衡

彩票的本质是一种“概率游戏”，其设计初衷是募集公益资金，而非投资工具，中奖概率极低，且每一期开奖独立，无法预测，彩民应避免以下误区：

• 赌徒谬误：认为“之前没开55555，下次更可能开”，每期概率重置。
• 热号冷号偏见：有些彩民追踪历史号码，试图找出“规律”，但随机序列中并无模式可言。
• 过度投入：购买彩票应以娱乐为主，而非寄望一夜暴富，国家彩票资金用于社保、体育事业等，返奖率约为50%（排列5为50%），长期参与必然亏损。

体彩开出“55555”的概率是十万分之一，与其他任何号码完全相同，这一事件之所以引人注目，源于心理认知偏差和投注集中度，而非概率异常，数学告诉我们：随机性既公平又“无情”，它允许多样化结果，包括极端值的出现，对于彩票，我们应以科学态度看待——享受其惊喜，但绝不沉迷，毕竟，人生中的真正幸运，往往来自努力与选择，而非随机数字的排列。